深入理解计算机系统 读书笔记 2.信息的展示和处理

本章导读

在构造存储和处理信息的机器时，二进制的值工作得更好。二进制信号可以很容易地被表示，存储和传输。例如，可以表示为穿孔卡片上有洞无洞、导线上的高电压和低电压。对二值信号进行存储和执行计算的电子电路非常简单可靠。

信息存储

机器级程序将存储器视为一个非常大的字节数组，称为虚拟存储器（virtual memory）。存储器的每个字节都有唯一的数字来标识，称为它的地址（address），所有可能地址的集合称为虚拟地址空间（virtual address space）。

C语言中一个指针的值（无论它是指向一个整数、一个结构或者其他程序对象） 都是某个存储块的第一个字节的虚拟地址。C编译器还把每个指针和它的类型信息结合起来，这样就能访问存储在指针所指向位置的值。

十六进制表示法

一个字节（byte）由8位（bit）组成。

在二进制表示法中，它的值域是 00000000-11111111

在十进制表示法中，它的值域是 0-255

在十六进制表示法中，它的值域是 00-FF

在C语言中，以0X或者0x开头的数字常量被认为是十六进制的值。字符'A'-'F'不区分大小写，甚至可以混写。

记住十六进制的数字 A，C，F 对应的十进制值，以便迅速完成进制转换计算。

数据大小

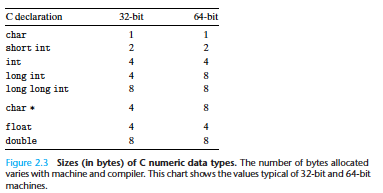
寻址和字节顺序

在几乎所有机器上，多字节对象都被存储为连续的字节序列，对象地址为所使用字节中最小的地址。例如，假设一个类型为int的变量x的地址为0x100，那么，地址表达式&x的值为0x100. x的4个字节将被存储在存储器的0x100，0x101，0x102和0x103.

假设变量x类型是int，位于地址ox100处，它的十六进制值是OX01234567。它的大端，小端表示法如下图。

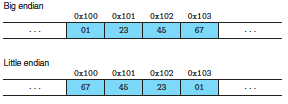
书中对“endian“不同选择的解释为“情绪化选择，没有技术上的原因”，我对这种解释表示不满，但是目前也没精力进一步考究

在通过网络传输数据以及在查看汇编代码时，需要数据的大端、小端的区别。

寻址和字节顺序

分别是 反，与，或，异或

布尔代数计算公式：

a^0=a

a^a=0

(a^b)^a=(a^a)^b=0^b=b


未去进一步证明(a^b)^a=(a^a)^b 这个交换律，话说加法交换律怎么证明的？这个链接未细看：http://www.guokr.com/post/438284/

C语言支持按位布尔计算。

C语言的移位计算

x<<k: x向左移动，丢弃最高的k位，并在右端补k个0

x>>k:

• 逻辑右移：左端补k个0
• 算术右移：左端补k个最高有效位（是指截取k个位后的数值的最高有效位）的值

C语言标准并没有明确定义应该使用哪种类型的右移。对于无符号数据，右移必须时逻辑的。对于有符号数据，几乎所有编译器、机器都是算术右移。

JAVA语言对右移进行了明确定义。x>>k 算术右移 x>>>k 逻辑右移

整数表示

整数数据类型

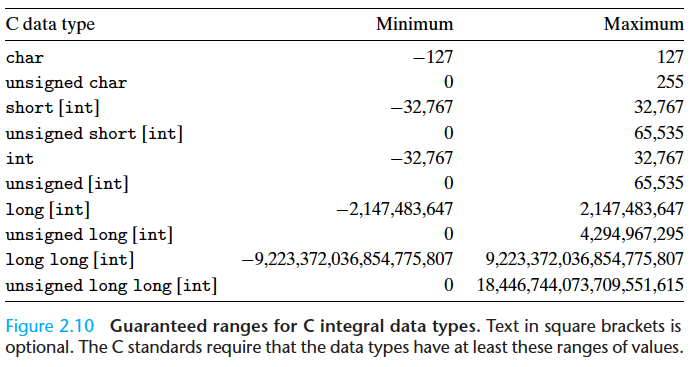
C语言标准要求这些数据类型至少具有这样的取值范围，负数和整数取值范围对称

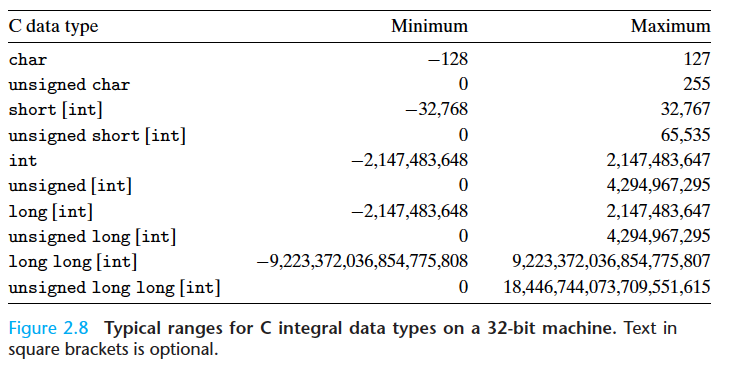
典型情况下（实际实现中），负数和整数取值范围不对称，负数比正数范围大一

C和C++都支持有符号（默认）和无符号数。Java仅支持有符号数。

无符号数/有符号数编码

无符号数向量到整数映射公式：

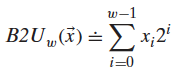
无符号数向量到整数映射示例：

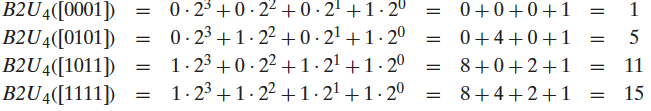
有符号数（补码形式，最高有效位为负权）向量到整数的映射公式：

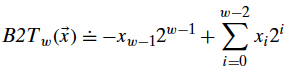
有符号数（补码形式）向量到整数的映射示例：

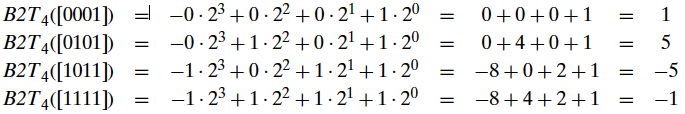
规律：

• UMax=2的w次方-1

• TMax=2的w-1次方-1

• TMin=-2的w-1次方

• |TMin|=TMax+1

• UMax=2TMax+1

无符号数/有符号数转换

强制类型转换的结果是保持位值不变，只是改变了解释这些位的方式。 -12345的16位补码表示和53191的补码表示值时一样的，均是OXCFC7.

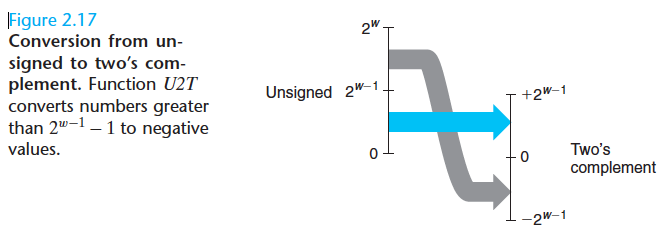
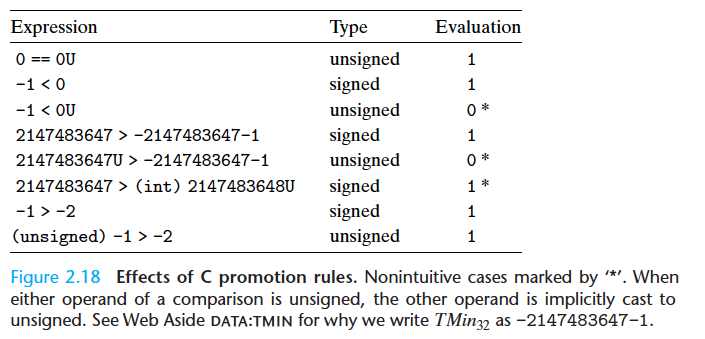
当执行一个运算时，如果它的一个运算符时有符号的而另一个是无符号数时，那么C语言会隐式地将有符号参数转为无符号数。

扩展一个数字的位

将一个无符号数转换为一个更大的数据类型，我们只需要在前面添加0，称之为零扩展（zero extension）

将一个补码数字转换为一个更大的数据类型，我们需要在前面添加最高有效位的值的副本，称之为符号扩展（sign extension）

1 short sx = -12345; /* -12345 */   2 unsigned uy = sx; /* Mystery! */  3   4 printf("uy = %u:\t", uy); 5 show_bytes((byte_pointer) &uy, sizeof(unsigned));
#运行结果是：uy = 4294954951: ff ff cf c7

注意（unsigned） sx 等价于 (unsigned)(int)sx ，求值是 4 294 954 951（先升位，后求值） ，而不等价于 （unsigned）（unsigned short ）sx，后者求值是 53191.

截断数字

对于一个无符号数字x，截断它到k位的结果为y，y= x mod 2的k次方 对于一个有符号数字x，截断它到k位的结果位y，y= x mod 2的k次方，不过需要把y的最高位解释为符号位。

整数运算

刚入门的程序员会发现，两个正数相加可能会得到一个负数，并且比较表达式 x<y 和 x-y<0 结果是截然不同的。

无符号加法

一些编程语言，如Lisp，实际上支持无限精度的运算，允许任意的（当然，要在机器的存储器范围之内）的整数运算。

更常见的是，比如java 和，只支持固定精度的运算。

对于两个非负整数x和y，满足0<=x，y<=2的w次方-1；x+y的范围是0<=x+y<=2的w+1次方-2

TIPS

大爱这句话：“请放心，每个掌握了高中代数知识的人都具备理解这些内容所需要的数学技能”。 当时看到这句话的时候，又增强了不少的信心。人生啊，就是不断地给自己打鸡血。